労働災害の発生状況の一考察
◎ ハインリッヒの1:29:300の法則をめぐって
アメリカの保険会社の技術者であったハインリッヒ氏が1931年に刊行した「災害防止の科学的研究」は,災害防止関係の古典として多くの人に読まれているが,氏はその中で災害防止に関するいくつかの法則を掲げている.
まず,基本的原則として,
① 安全に対する関心の喚起とその持続
② 事実の調査
③ 事実に基づいた是正措置
をあげ,
さらに 産業安全の原理として,
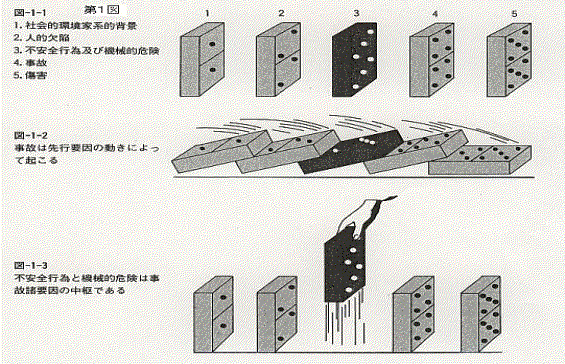
① 災害は完結し,相関連する要素から起こる.このうちの一つの要素は,事故そのものである.
② 事故は人の不安全行為及び機械的または物理的危険のうちの一つ,あるいは両方の事情が先行するかまたは同時に起こり,これが直接の原因として人が傷つく場合に限って発生する.
③ 人の不安全行為または機械的あるいは物理的危険は,ただちに事故または負傷の原因となるとは限らない.
④ 負傷の程度は多くの場合,偶発的である.
⑤ 災害防止に最も価値ある方法は生産の品質,コストおよび数量を支配する方法とよく似ている.
等を述べている.
また,事故の要素とその相関として5つの駒を時系列的に並べたドミノを提唱し,要素の中で不安全行為と機械的危険をその中枢であるとした(第1図).
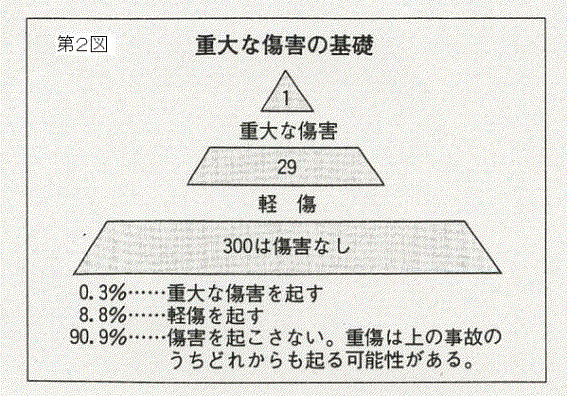
また、多数の工場での調査結果から重大な傷害と軽傷と傷害の発生がなかった事故との間にはその数で1:29:300の比率の関係があることを実証した.これが有名な1:29:300の法則である(第2図).
さらに、1969年に北アメリカ保険会社で行われた1,753,498の災害報告を対象にする調査では,重篤な傷害と軽微な傷害と物的損害と損害を伴わないインシデントとの間に1:10:30:600という比率があることが報告されている.
これらの比率はその数字に意味があるのではなく,このような考え方が大切であると思われる.(ちなみに,日本の建設業で発生した労働災害をとってみると,傷害の発生しなかった事故の数はわからないが,死亡と休業4日以上の災害の比率は建設業全体で約1:30である.)
そこで,発生した災害を分析することによって,この考え方が適用できるか,適用できるとした場合例えば,物を高所で作業中の労働者が取り落とし,その下方に労働者がいたような場合,下の労働者にあたれば怪我をするだろうし,当りどころが悪ければ死亡災害になるかもしれない,あたらなければ単なる出来事(これをハインリッヒは事故(ACCIDENTS)と言っている.)で終わるというように,その出来事が1:29:300のいずれに属することとなるかはきわめて確率的であるはずであるから,その状況はどのようになっているかを明らかにしようとした.
○ 災害発生の分布はどのようになっているか
まず最初に,1:29:300の法則が成り立つためには,災害発生の確率分布が発生数が少ない場合には,機械などの故障の発生や,不良製品の発生の場合にみられるポアッソン分布となるはずである.
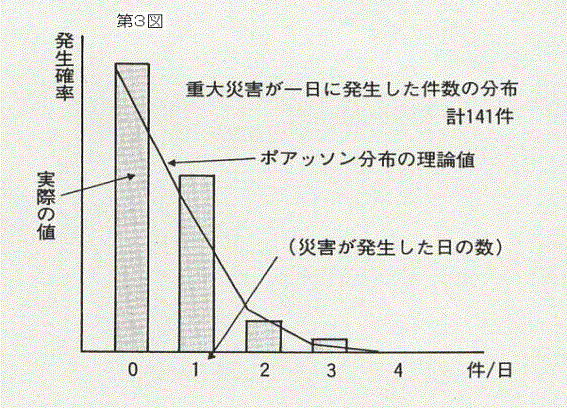
例として,重大災害(一時に3名以上の死傷者を生じた災害をとって,1日に発生した災害の度数の分布(何件の災害が発生した日が何日あるかの分布)を第3図に示したが,重大災害や休業災害でも発生数が少なければ同様の結果が得られる
この分布はポアッソン分布の理論値(多くの独立した要素から希に発生する事柄の確率の分布)とほぼ同じである.
したがって,災害は多くの要素からなり,その発生は確率的であることがいえる。
災害発生の分布のばらつきはどのようになっているか.
次に,災害発生が確率的であるならばその分布はどのようになっているのであろうか,日本の建設業における死亡災害について次のようなステップで分析を行ってみた.
① 10年間の日本の建設業で発生した死亡災害を分析の対象とした.
② 1件の出来事で複数の死亡者を生じた災害は1件とした.
③ 各年について1月1日から12月31日までの毎日にそれぞれ何件の災害が発生したかを調べた.
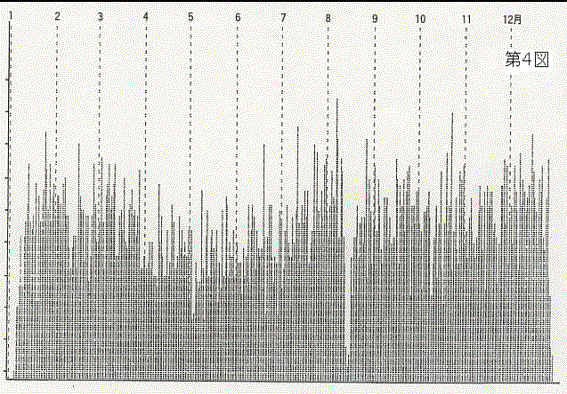
④ うるう年の2月29日を除いて,8年分を各月日ごとに累積した.(第4図)
これは,意味がある変化を見いだすためであり,併せて,日ごとの平均値と標準偏差を計算した.
⑤ 平均値から標準偏差を2倍した値を引いた値より小さい値の日(12月30日から1月4日までと8月14日から16日までが該当した)を各年のデータから除いた.(平均値に標準偏差を2倍した値を加えた値より大きい日を除こうとしたが該当するものがなかった.)
⑥ 各年の曜日ごとの発生件数を調べた.この結果,日曜日を除いて意味がある差は見いだせなかった.(曜日ごとの災害発生のグラフ参照)
各年のデータから日曜日を除いた.
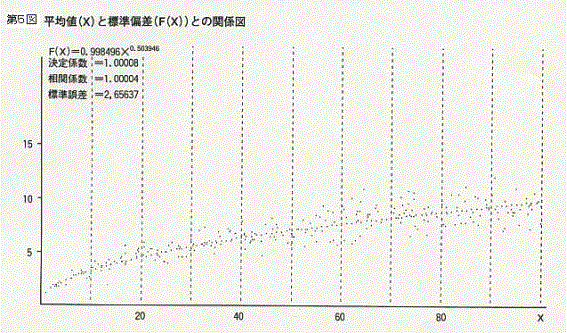
⑦ 各年の日ごとのデータを1月から12月まで並べ,コンピュウタで乱数をつくり,その乱数にしたがって各年ごとに日を選び,その日の集まりの合計を1日から100日まで順次増加してゆき,それぞれについて100以上のデータにより平均値とそれに対応する標準偏差とを計算してグラフにした.(第5図)
⑧ このグラフのデータを用いて,指数回帰を行い,標準偏差と平均値との関係を示す方程式を決定した.
その式は,標準偏差=平均値の平方根 というものであり,この式の決定係数はほとんど1であった.
分析の結果言えること
災害の確率の分布がポアッソン分布であり,平均値と標準偏差との関係が平方根にしたがうことは,予想された通りであったが,このことから実際の応用として言えることは,
まず第一に,災害には多くの要因がありそれが傷害や死亡を産むのはきわめて確率論的であるから,災害防止のためには災害の要因(ポテンシャルとも呼ばれる)を除く努力が大切である.
つぎに,例えばある会社で年間10件の災害があるとすると,その災害件数には,プラスマイナス10の平方根(3.2)の偏差がついているのであるから,そのことを十分に考慮して,この値の評価をすべきであること.
災害を数量的に分析するときにおいても同様である.
さらに、災害の要因をかたまりとして認識する場合(一般的には事故の型、起因物、不安全な状態、不安全な行動等)適用されなければならない理論があるが別に述べる。
注)第一図及び第2図はハインリッヒの原著から引用し翻訳した。